Die einfachste Schwingungsform liegt mit der harmonischen oder sinusförmigen Schwingung vor, die man mit einem mathematischen Pendel oder mit bestimmten Schallquellen, z.B. einer Stimmgabel erzeugen kann.
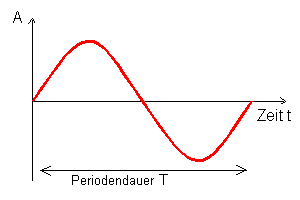
Trägt man den Verlauf einer sinusförmigen Schwingung über der Zeit auf, so erhält man einen typischen Verlauf, der eindeutig durch die Größen
- Periodendauer T : zeitliche Dauer eines Schwingungsverlaufs
- Amplitude A: Maximale Auslenkung der Schwingung
- Phase j: Startpunkt der Schwingung, bzw. zeitliche Verschiebung zweier Schwingungsverläufe zueinander
Aus Gründen der Handhabbarkeit wird statt der Periodendauer T die Frequenz f zur Beschreibung der Schwingungsanzahl pro Sekunde verwendet. Diese ergibt sich direkt aus dem Kehrwert der Periodendauer:
- Frequenz f : f = 1/T : Schwingungsanzahl pro Sekunde. Die Einheit der Frequenz ist das Hertz [Hz]
Der zeitliche Verlauf einer Sinusschwingung ist in der nebenstehenden Grafik dargestellt. Bei Überfahren mit der Maus wird eine zweite, phasenverschobene Schwingung sichtbar.
Eigene Versuche zum Einfluß der Parameter Amplitude und Fequenz auf den Verlauf einer Sinusschwingung können sie mit dem
vornehmen.